The note is partially based on the Bayesian Nonparametrics Machine Learning lectures by Yee Whye Teh at Max Planck Institute for Intelligent Systems in Tübingen, Germany.
Machine learning is all about data, and the uncertainty and complex process in the data. Probability theory is a rich language to express uncertainties. Graphical tool and complex models are develped to help visualize and derive algorithmic solutions.
Probabilistic Modelling
- Data: $x_1, x_2, …, x_n$
- Latent variables: $y_1, y_2, …, y_n$
- Parameter: $\theta$
- Probabilistic model (generative model): parametrized joint distribution over variables
$P(x_1, x_2, …, x_n, y_1, y_2, …, y_n|\theta)$ - Inference, of latent variables given observed data:
$P(y_1, y_2, …, y_n|x_1, x_2, …, x_n, \theta) = \frac{P(x_1, x_2, …, x_n, y_1, y_2, …, y_n|\theta)}{P(x_1, x_2, …, x_n|\theta)}$ - Learning, of parameters by maximum likelihood:
$\theta^{ML} = \underset{\theta}{\text{argmax }}P(x_1, x_2, …, x_n|\theta) $ - Prediction: $P( x_{n+1}, y_{n+1} |x_1, x_2, …, x_n,\theta)$
- Classification: $\underset{c}{\text{argmax }}P(x_{n+1}|\theta^c) $
Bayesian Modelling
- Prior distribution: $P(\theta)$
- Posterior distribution (both inference and learning):
$P(y_1, y_2, …, y_n,\theta |x_1, x_2, …, x_n) = \frac{P(x_1, x_2, …, x_n, y_1, y_2, …, y_n|\theta) P(\theta) }{ P(x_1, x_2, …, x_n) }$ - Prediction: $P( x_{n+1}| x_1, x_2, …, x_n) = \int P( x_{n+1}|\theta )P(\theta| x_1, x_2, …, x_n )d\theta $
- Classification: $P( x_{n+1}^c| x_1^c, x_2^c, …, x_n^c) = \int P( x_{n+1}|\theta^c )P(\theta^c| x_1^c, x_2^c, …, x_n^c )d\theta^c $
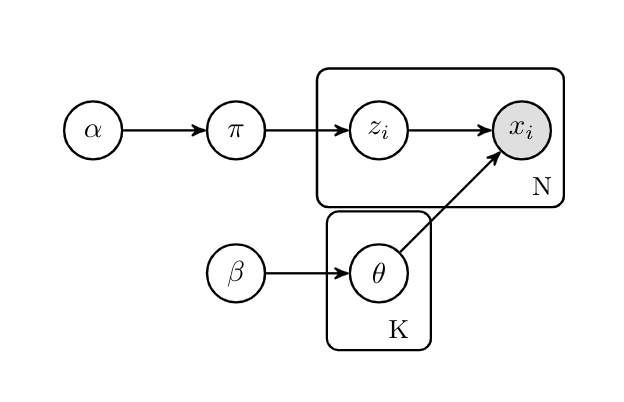
Model-based Clustering
Given data from heterogeneous unknown sources, and each cluster modelled using a parametric model:
- Data item:
$z_i|\pi\sim \text{Discrete}(\pi)$
$x_i|z_i,\theta_k \sim F(\theta))$ - Mising proportions: $\pi = (\pi_1, \pi_2,…, \pi_K)|\alpha \sim \text{Dirichlet}(\alpha/K,…, \alpha/K)$
- Cluster k: $\theta_k|\beta \sim \beta$
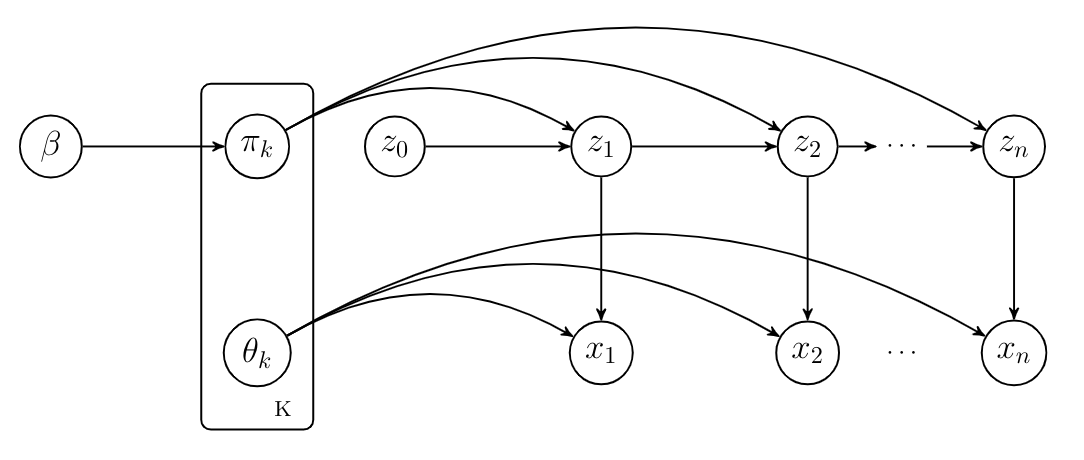
Hidden Markov Models
- Popular model for time series data (clustering over time)
- Unobserved dynamic modelled using a Markov model
- Observations modelled as independent conditioned on current state
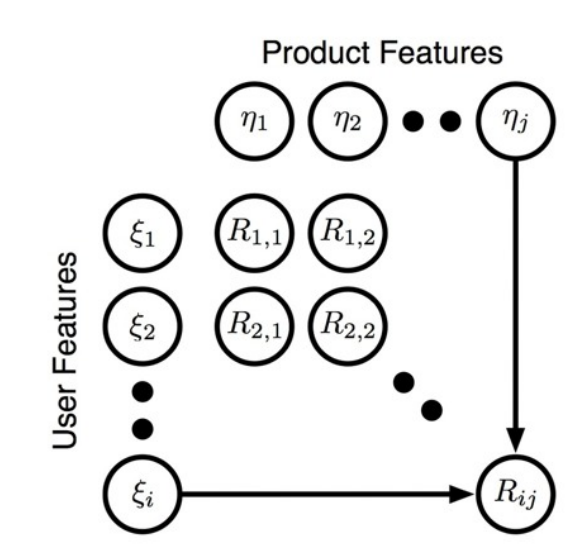
Collaborative Filtering
A kind of recommendation system. e.g.: predict how much users would like products that they haven’t seen based on the previous data.
Data: Rating $R_{ij}$ of a user $\xi_i$ for a certain product $\eta_j$
$R_{ij}|\xi_i,\eta_j \sim \mathcal{N}(\xi_i^\top \eta_j, \sigma^2) $
Bayesian Nonparametrics
As I discussed in the previous blog post (Why are Gaussian Process Models called Nonparametric?), nonparametric model is a parametric model where the number of parameters increases with data. It just cannot be described by fixed number of parameters. And nonparametric models still make model assumptions, but they are less constrained.
Why do we want Bayesian nonparametrics?
- Model Selection:
Typically we use parametric model, say clustering, we need to decide the number of clusters. If we have too many clusters we would encounter overfitting issue, and underfitting if we have too little clusters. In Bayesian model we don’t do model optimization to find the maximum likelihood parameters for the optimal number of clusters, we just compute posterior distribution for the unknown part. And the Bayesian nonparametric model grows with amount of data, thus we can prevent overfitting and underfitting issues. - Large Function Spaces:
We would like to learn the large function space and infer the infinite dimensional objects themselves, and we want to learn the density of the input space. - Structural Learning:
We want to learn the structures of the data (e.g. hierarchical clustering), and we can use bayesian prior over combinatorial structures. Commonly, nonparametric priors alwayes lead to simpler learning algorithm than parametric priors because you don’t need to worry about complicated model selection (e.g. number of latent variables, the way of latent variables connecting to other variables etc.). - Novel & Useful Properties
- Exchangeability: permute your dataset without effecting the analysis
- Power laws behaviors: Pitman-Yor process, Indian Buffet process
- Flexible to build complex models: hierarchical nonparametric models, dependent Dirichlet process
Dirichlet Process
Dirichlet process is the cornerstone of modern Bayesian nonparametrics. It is the infinite limit of finite mixture models. It was defined by Ferguson in 1973 as a distribution over measures.
Finite Mixture Models
Dirichlet distrbution on K-dimensional probability simplex $\{\pi | \sum_k \pi_k=1 \}$:
$P(d\pi| \alpha) = \frac{\Gamma (\alpha)}{\Pi_k\Gamma(\alpha/K)}\Pi_{k=1}^K \pi_k^{\alpha/K-1}d\pi \quad$ with $\Gamma (\alpha) = \int_0^\infty x^{\alpha -1} e^x dx$
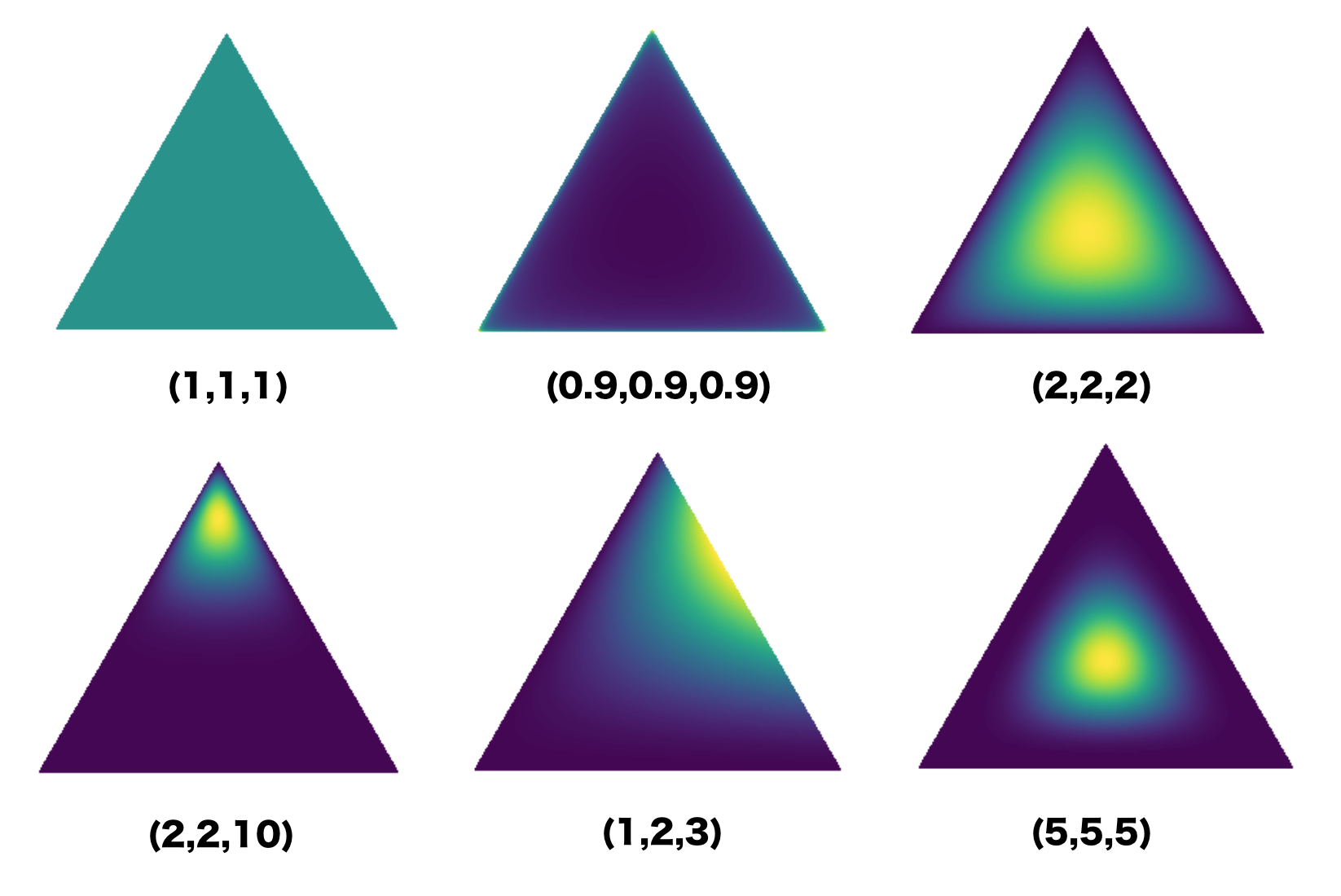
See Model-based Clustering part in the previous section. Given the observations $\mathbf{x}$ we want to learn the latent variables $\mathbf{z}, \pi, \mathbf{\theta}$. We can use MCMC sampling to infer the unknown parameters. We are constructing a Markov chain such that we can do the inference in an iterative manner as the chain would converge at some point.
Gibbs Sampling

- Calculate the conditional distribution of the latent variables given the parameters and the observations: $ p(z_i=k|\text{ others }) \propto \pi_k f(x_i |\theta_k^*) $
$ \pi|\text{ others } \sim \text{Dirichlet}(\frac{\alpha}{K}+n_1,…, \frac{\alpha}{K}+n_K) $ - Calculate the conditional distribution of the parameters given the latent variables and the observations: $ p(\theta_k^*=\theta|\text{ others }) \propto B(\theta)\Pi_{j:z_j=k} f(x_j |\theta) $
- Iterate this process until they (latent variables and parameters) converge to the posterior distribution.
Collapsed Gibbs Sampling
A more efficient approach of MCMC argorithm: integrate out $\pi, \theta^*$
- Marginalize out the parameters of the model
- All we don’t know is the latent variable (the clusters), and now we have the reduced space to update.
$ p(z_i=k|\text{ others }) \propto \frac{\frac{\alpha}{K} + n_k^{-i}}{\alpha+n-1}f(x_i|z_j=k)$
where $ f(x_i|z_j=k) \propto \int B(\theta)f(x_i|\theta)\Pi_{j\neq i: z_j = k} f(x_j|\theta)d\theta $
The prior term $\frac{\frac{\alpha}{K} + n_k^{-i}}{\alpha+n-1}$ is interpretable, $n_k^{-i}$ denotes the number of other data iterms currently assigned to cluster $k$ besides the current item $i$ we are interested in. $\frac{\alpha}{K}$ means even no item belongs to cluster $k$, we still have some probability for cluster $k$. The likelihood $f(x_i|z_j=k)$ means the conditional probability of the observation given the observations that are currently assigned to cluster $k$ - Conditional distributions can be easily computed if $F$ is conjugate to $B$.
Infinite Limit of Collapsed Gibbs Sampling
Assume a very large varlue of $K \rightarrow \infty$, there are at most $n<K$ occupied clusters (most components are empty). We can combine these empty components together:
$ p(z_i=k|\text{ others }) = \frac{n_k^{-i}+ \frac{\alpha}{K}}{n-1+\alpha}f(x_i|z_j=k)$
$ p(z_i=k_{empty}|\text{ others }) = \frac{\alpha\frac{K-K^*}{K}}{n-1+\alpha}f(x_i|\{\})$
When $K \rightarrow \infty$, we get:
$ p(z_i=k|\text{ others }) = \frac{n_k^{-i}}{n-1+\alpha}f(x_i|z_j=k)$
$ p(z_i=k_{empty}|\text{ others }) = \frac{\alpha}{n-1+\alpha}f(x_i|\{\})$
- The actual infinite limit of the finite mixture model has problems: any particular cluster will get a mixing proportion of 0.
- Better way for the infinite limit thinking:
- Chinese restaurant process
- Stick-breaking construction
- Both are infinite dimensional Dirichlet distributions of Dirichlet Process(DP)
Chinese Restaurant Process
Partitions
A partition $\varrho$ of a set $S$ is
- A disjoint family of non-empty of subsets $S$ whose union in $S$
- e.g. $S = \{ A,B,C,D,E,F,G \}$
- e.g. $\varrho = \{ \{A\},\{B,C\},\{D,E,F,G\} \}$
- The set of all partitions of $S$ is $\mathcal{P}_S$
- Random partitions are random variables taking values in $\mathcal{P}_S$
Chinese Restaurant Process
- Each customer comes into restaurant and sits at a table
$P(\text{sit at table }c) = \frac{n_c}{\alpha+\sum_{c\in \varrho} n_c} $
$P(\text{sit at new table}) = \frac{\alpha}{\alpha+\sum_{c\in \varrho} n_c} $ - Customers correspond to element $S$, tables correspond to clusters in $\varrho$
- Rich-gets-richer: larger clusters are more likely to attract more customers
- Multiplying conditional probabilities together, the overall probability of $\varrho$ (exchangeable partition probability function (EPPF)) is
$P(\varrho|\alpha)=\frac{\alpha^{|\varrho|}\Gamma(\alpha)}{\Gamma(n+\alpha)}\Pi_{c\in \varrho} \Gamma(|c|) $
The distribution over the partition does not relate to the order of the customers enter the restaurant, and it only depends on the number of the clusters and the size of the clusters.
Number of Clusters
The prior mean and variance of $K$ are:
$ E[ \rho| \alpha, n ] = \alpha(\psi(\alpha+n)-\psi(\alpha))\approx \alpha \text{ log}(1+\frac{n}{\alpha}) $
$ V[ \rho| \alpha, n ] = \alpha(\psi(\alpha+n)-\psi(\alpha)) + \alpha^2(\psi’(\alpha+n) - \psi’(\alpha)) \approx \alpha \text{ log}(1+\frac{n}{\alpha}) $
where $\psi(\alpha) = \frac{\partial }{\partial \alpha}\text{ log }\Gamma(\alpha)$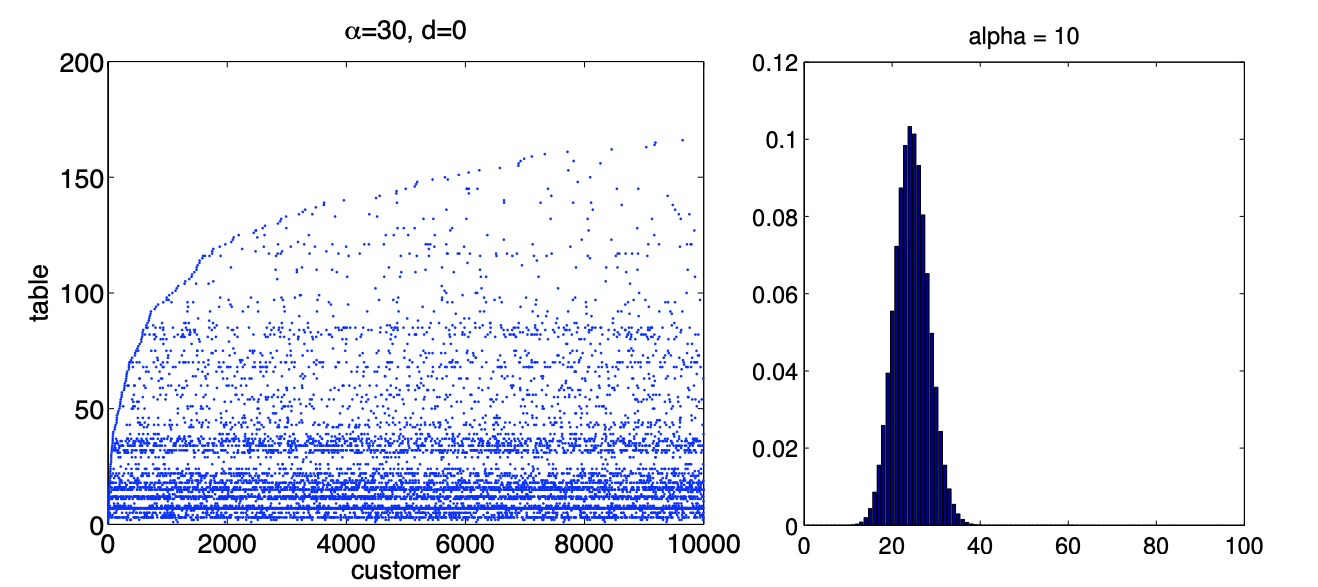
CRP Mixture Model
Given a dataset $S$, we want to partition it into clusters of similar items. And we can use CRP prior over partitioins $\varrho$.
- $\varrho\sim \text{CRP }(\alpha)$
- $\theta^*|\varrho \sim H \text{ for } c\in \rho$
$x_i|\theta,\varrho \sim F(\theta_c^*) \text{ for }c\in \varrho \text{ with } i\in c$
CRP prior over $\varrho$, iid prior $H$ over cluster parameters
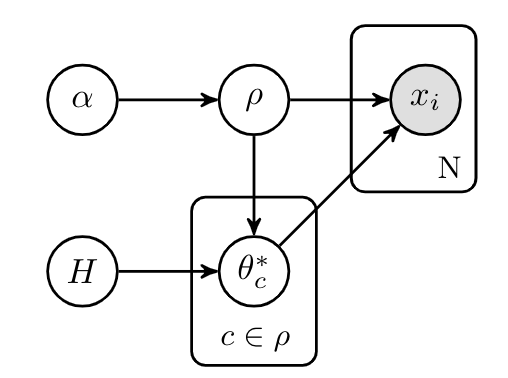
CRP can thus induce distribution over partitions:
- $P(\mathbf{z}|\alpha) = \frac{\Gamma(\alpha)}{\Pi_k\Gamma(\alpha/K)}\frac{\Pi_k\Gamma(n_k+\alpha/K)}{\Gamma(\alpha+n)}$ describes a partition of the data set into clusters, and a labelling of
each cluster with a mixture component index. - Induces a distribution over partitions $\varrho$ (without labelling) of the data set:
$P(\varrho|\alpha) = [K]^k_{-1}\frac{\Gamma(\alpha)}{\Gamma(\alpha+n)} \Pi_{c\in\varrho} \frac{\Gamma(|c|+\alpha/K)}{\Gamma(\alpha/K)}$ - Assume $K\rightarrow \infty$ (maximum number of clusters in our partitions), we get a proper distribution over partitions without a limit on the number of clusters:
$P (\varrho|\alpha) \rightarrow \frac{\alpha^{|\varrho|}\Gamma(\alpha)}{\Gamma(\alpha+n)} \Pi_{c\in\varrho} \Gamma(|c|)$ - So the induced distribution over partitions approach Chinese Restaurant Process.
- $P(\mathbf{z}|\alpha) = \frac{\Gamma(\alpha)}{\Pi_k\Gamma(\alpha/K)}\frac{\Pi_k\Gamma(n_k+\alpha/K)}{\Gamma(\alpha+n)}$ describes a partition of the data set into clusters, and a labelling of
In Chinese Restaurant Process is the distribution over partitions of a collection of objects, which can be used to build nonparametric model-based clustering models. It is related to the infinite limit of finite mixture models (solve the limitation of the originial infinite models).
Reference
[1] Bayesian Nonparametrics Fandom Page
[2] Visualizing Dirichlet Distributions with Matplotlib
[3] Bayesian Nonparametrics 1 - Yee Whye Teh - MLSS 2013 Tübingen